2019-2020学年度上海清流中学初中三年级（上）首次月考数学考试试题
（满分 150分，考试时间 100分钟）
选择题；（本大题共6题，每题4分，满分24分）
1.若mn=pq，则下列比率式正确的是（ ）
（A）
（B）
（C）
（D）
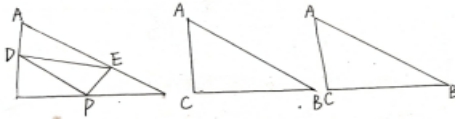
2.如图，△ABC中，D、E是边AB、AC上点，且DE∥BC，则下列等式中成立的是（ ）
（A）
（B）
（C）
（D）
3.已知线段a，b，c；求作线段x，使得a：b=c：x，下列作图正确的是（ ）
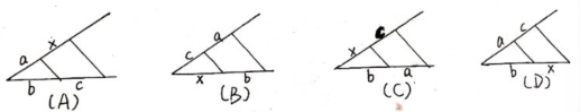
下列条件中，能判断两个等腰三角形一样的是（ ）
（A）都含有一个30°的内角 （B）都含有一个45°的内角
（C）都含有一个60°的内角 （D）都含有一个80°的内角
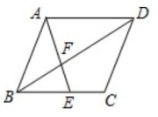
5.对于△ABC与△DEF，可由∠A=∠D和下列某一个条件推的△ABC∽△DEF，这个条件是（ ）
（A）
（B）
（C）
（D）
6.下列说法中，正确的个数是（ ）
①假如一条直线截三角形两边的延长线所得的对应线段成比率，那样这条直线肯定平行于三角形的第三边；
②邻边相等的两个平行四边形肯定相似；
③相似三角形的中线的笔等于相似比；
④通常来讲，一条线段的黄金分割点有两个；
⑤两条直线被第三条直线所截，所截得的线段对应成比率，则这三条直线肯定平行；
（A）1个 （B）2个 （C）3个 （D）4个
2、填空题：（本大题共12题，每题4分，满分48分）
7.假如
，那样x=_________.
8.线段9和25的比率中项是_________.
9.上海与南京的实质距离约450千米，在比率尺为1:5 000 000的地图上，上海和南京的图上距离约_________厘米.
10.如图，平行四边形ABCD中，E是边BC上的点，AE交BD于点F，假如BE：BC=2:3，那样BF：BD=________.
如图，梯形ABCD中，点E、F分别在边AB、DC上，AD∥BC∥EF，BE：EA=1:2，假如AD=2，BC=5，那样EF=________.
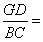
如图，l1∥l2∥l3，AB=4，DF=8，BC=6，则DE=________.
在△ABC中，点D、E分别在△ABC的边AB、AC上，DE∥BC，
，四边形DBCE的面积比△ADE的面积大28，，则△ABC的面积是________.
如图，若点G是△ABC的重点，GD∥BC，则________.
如图，正△ABC中，P为BC上一点，D为AC上一点，∠APD=60°，BP=1，CD=
，则△的边长为________.
如图，请在方格图中画出一个与△ABC相似且相似比不为1的三角形（它的顶点需要在方格图的交叉点上）.
在△ABC和△DEF中，∠A=∠D，AB=4，BC=5，AC=6，EF=10，假如△ABC与△DEF相似，那样DE=________.
在Rt△ABC中，∠ACB=90°，AB=10，BC=8，G为△ABC的重点，过点G的直线截△ABC，交AC边于点D，交BC边于点E，若△CDE与△ABC相似，则BE的长为________.
3、解答卷（第19-22题每题10分，第23-24题每题12分，第25题14分）
（本题10分）已知，x：y：z=2：3：4，求：
的值；（2）若x+y+z=18，求x，y，z。
（本题10分）如图， ABCD中，点E在BA的延长线上，联结EC交AD于点F，交对角线BD与点G，求证：
.
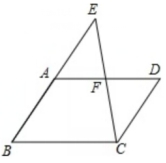
21.（本题10分）如图，在△ABC中，点D、E分别在BC、AC上，BE平分∠ABC,DE∥BA，假如CE=6，AE=4，AB=15，求DE和CD的长。
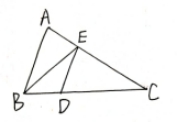
22.（本题10分）如图，BD、CE为△ABC的高，求证：△AED∽△ACB。
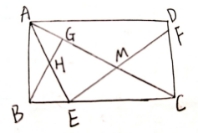
（本题12分）已知：如图，点E是矩形ABCD的边BC上一点，EF⊥AE，EF分别交线段AC、CD于点M、F，BG⊥AC，垂足为G，BG交AE于点H.
求证：△ABE∽△ECF：
找出与△ABH一样的三角形，并证明：
若点E是BC的中点，BC=2AB，AB=2，求AM的长.
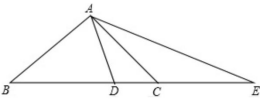
（本题12分）已知△ABC，D、E是射线BC上的两点，且BD=AB，CE=AC。
AB=AC，且∠BAC=90°（如图16），求证AE2=BEDE：
若△ABC是直角三角形，且AE2=BEDE，求∠ABC的度数。（假如需要，自己画出符合条件的大致图形）
25.（本题14分，其中第（1）小题4分，第（2）小题5分，第（3）小题5分）
已知：在Rt△ABC中，∠ACB=90°，AC=3，BC=4，点P是边BC的中点，点D、E分别是射线AC、射线BA上一个动点，且∠DPE=90°，联结DE，设BE=x，CD=y.
如图1，当D、E分别在边AC、边BA上时，试求y关于x的函数关系式，并写出它的概念域.
若△BEP为等腰三角形，求出cd的长.
若△DEP与△ABC相似，求出AD的长.
